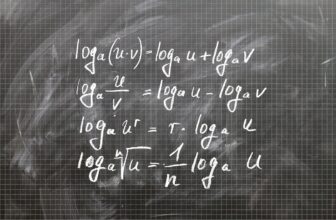Cálculo numérico y métodos aproximados
El cálculo numérico es una disciplina que se ocupa de desarrollar métodos y técnicas para realizar cálculos aproximados de problemas matemáticos. Estos métodos son especialmente útiles cuando las soluciones exactas son difíciles o imposibles de obtener, o cuando se necesita realizar cálculos con una gran cantidad de datos. En este artículo, exploraremos los fundamentos del cálculo numérico y los métodos aproximados, analizando su importancia y aplicación en diversas áreas de estudio.
¿Qué es el cálculo numérico?
El cálculo numérico se refiere al proceso de realizar cálculos matemáticos utilizando técnicas aproximadas en lugar de soluciones exactas. Esto implica el uso de algoritmos y métodos que permiten obtener resultados cercanos a la solución real, pero no necesariamente idénticos. El cálculo numérico es especialmente útil cuando las soluciones exactas son difíciles o costosas de obtener, o cuando se trabaja con datos experimentales o mediciones.
Métodos aproximados en cálculo numérico
Existen varios métodos aproximados utilizados en el cálculo numérico para resolver problemas matemáticos. Algunos de los métodos más comunes incluyen:
Método de Newton-Raphson:
Este método se utiliza para encontrar las raíces de una ecuación no lineal. Se basa en una sucesión de aproximaciones que convergen hacia la solución real. El método de Newton-Raphson utiliza la derivada de la función para calcular iterativamente una mejor aproximación de la raíz.
Método de interpolación:
La interpolación es utilizada para estimar valores desconocidos entre puntos conocidos. El método de interpolación se basa en la construcción de una función que pasa a través de los puntos de datos conocidos, y luego se utiliza esta función para estimar los valores en puntos intermedios.
Método de cuadratura numérica:
La cuadratura numérica se utiliza para aproximar el valor de una integral definida. Existen diferentes métodos de cuadratura numérica, como la regla del trapecio y la regla de Simpson, que dividen el intervalo de integración en subintervalos y aproximadamente calculan el área bajo la curva.
Aplicaciones del cálculo numérico
El cálculo numérico tiene una amplia gama de aplicaciones en diversas áreas. Algunas de las áreas donde se utiliza el cálculo numérico incluyen:
Simulaciones científicas:
En física, química y otras disciplinas científicas, el cálculo numérico se utiliza para simular fenómenos físicos complejos. Estas simulaciones permiten estudiar y comprender el comportamiento de sistemas físicos en condiciones difíciles de reproducir experimentalmente.
Procesamiento de señales e imágenes:
En el procesamiento de señales e imágenes, el cálculo numérico se utiliza para realizar operaciones como filtrado, compresión y reconstrucción de datos. Estos métodos aproximados permiten manipular y analizar señales y imágenes digitales de manera eficiente.
Finanzas y economía:
En el ámbito financiero y económico, el cálculo numérico se utiliza para realizar cálculos financieros, como la valoración de opciones, el análisis de riesgos y la optimización de carteras de inversión. Estos cálculos aproximados son fundamentales para la toma de decisiones en el ámbito financiero.

Desafíos en el cálculo numérico
Aunque el cálculo numérico es una herramienta poderosa, también presenta desafíos que deben ser considerados. Algunos de estos desafíos incluyen:
Estabilidad numérica:
Algunos métodos numéricos pueden ser inestables y producir resultados inexactos debido a errores de redondeo y propagación de errores. Es importante evaluar la estabilidad numérica de los métodos y tomar medidas para minimizar los errores.
Convergencia:
Algunos métodos numéricos pueden requerir un número excesivo de iteraciones para converger hacia la solución deseada. La elección de un método que converge rápidamente hacia la solución es fundamental para garantizar eficiencia en los cálculos.
Eficiencia computacional:
El cálculo numérico puede requerir una gran cantidad de recursos computacionales, como tiempo de procesamiento y memoria. Es importante desarrollar algoritmos eficientes que minimicen el consumo de recursos y mejoren el rendimiento de los cálculos.
El cálculo numérico y los métodos aproximados son herramientas fundamentales en el ámbito de las matemáticas y las ciencias de la computación. Estos métodos permiten obtener soluciones aproximadas a problemas matemáticos complejos, donde las soluciones exactas pueden ser difíciles o imposibles de obtener. El cálculo numérico tiene aplicaciones en diversas áreas, desde la física y la química hasta las finanzas y la economía. A medida que avanzamos en el ámbito de la computación, el desarrollo y la mejora de métodos numéricos seguirá siendo un campo activo de investigación y aplicación práctica.